什么是正交试验设计法？正交试验设计方法简介

正交实验设计法(Orthogonal Experimental Design )是指从大量的实验点中挑选出适量的、有代表性的点，依据Glois理论导出“正交表”。从而合理地安排实验的一种实验设计方法。正交实验设计法是研究多因素多水平的一种实验方法，生物学中经常会用这种方法研究植物的生长状况，一株植物的生长状况会受到多种因素的影响，包括种子质量等内部因素，还包括阳光、空气、水分、土壤等外部因素。在软件测试中，如果软件比较复杂，也可以利用正交实验设计法设计测试用例对软件进行测试。

正交实验设计法包含3个关键因素，具体如下所示。

(1)指标：判断实验结果优劣的标准。

(2)因子：因子也称为因素，是指所有影响实验指标的条件。

(3)因子的状态：因子的状态也叫因子的水平，它指的是因子变量的取值。

利用正交实验设计法设计测试用例时，可以按照如下步骤进行。

(1)提取因子，构造因子状态表

分析软件的规格需求说明得到影响软件功能的因子，确定因子可以有哪些取值，即确定因子的状态。例如，某一软件的运行受到操作系统和数据库的影响，因此影响其运行是否成功的因子有操作系统和数据库2个，而操作系统有Windows、Linux、Mac3个取值，数据库有MySQL、MongoDB、Oracle3个取值，因此操作系统的因子状态为3，数据库因子-状态为3。据此构造该软件运行功能的因子-状态表，如下表所示。

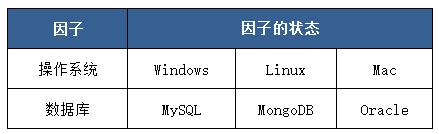
表 1

(2)加权筛选，简化因子-状态表

在实际软件测试中，软件的因子及因子的状态会有很多，每个因子及其状态对软件的作用也大不相同,如果把这些因子及状态都划分到因子-状态表中，最后生成的测试用例会相当庞大，从而影响软件测试的效率。因此需要根据因子及状态的重要程度进行加权筛选，选出重要的因子与状态，简化因子-状态表。

加权筛选就是根据因子或状态的重要程度、出现频率等因素计算因子和状态的权值，权值越大，表明因子或状态越重要，而权值越小，表明因子或状态的重要性越小。加权筛选之后，可以去掉一部分权值较小的因子或状态，使得最后生成的测试用例集缩减到允许的范围。

(3)构建正交表，设计测试用例

正交表的表示形式为L_n(t^c)。

·L表示正交表。

·n为正交表的行数，正交表的每一行可以设计一个测试用例，因此行数n也表示可以设计的测试用例的数目。

·c表示正交实验的因子数目，即正交表的列数，因此正交表是一个n行c列的表。

·t称为水平数，表示每个因子能够取得的最大值，即因子有多少个状态。

例如L₄(2³)是最简单的正交表,它表示该实验有3个因子，每个因子有两个状态，可以做4次实验，如果用0和1表示每个因子的两种状态，则该正交表就是一个4行3列的表，如下表所示。

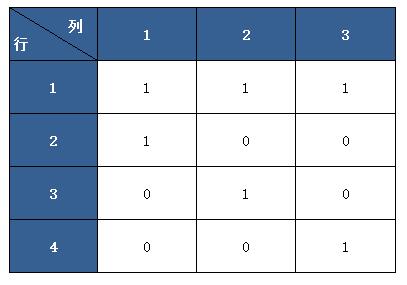
表2

假设表2中的3个因子为登录用户名、密码和验证码，用户名、密码和验证码有正确(用1表示)和错误(用0表示)两种状态，正常需要设计2³=8个测试用例，而使用正交表只需要设计4个测试用例就可以达到同样的测试效果。因此，正交实验法是一种高效、快速、经济的实验设计方法。

在表2中，3个因子的状态都有两种，这样的正交实验比较容易设计正交表，但在实际软件测试中，大多数情况下，软件有多个因子，每个因子的状态数目都不相同，即各列的水平数不等，这样的正交表称为混合正交表，如L₈(2⁴×4¹)，这个正交表表示有4个因子有2种状态，有1个因子有4种状态。混合正交表往往难以确定测试用例的数目，即n的值，这种情况下，大家可以登录正交表的一些权威网站，查询n值，例如，图下展示的是一个正交表查询网站的主页。

在这里，大家可以查询到不同因子数、不同水平数的正交表的n值。在该网站查找到2⁴×4¹的正交表n值为8，其正交表设计如表3所示。

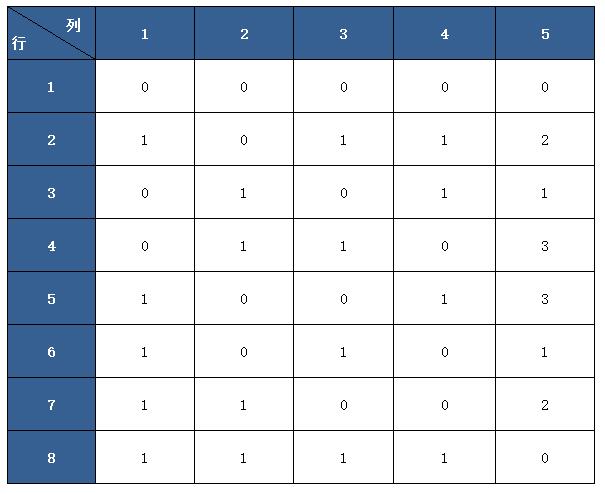
表3

由表3可知，第1～4列有0和1两种状态，第5列有4种状态，正符合“有4个因子有2种状态，有1个因子有4种状态”。

正交表最大的特点是取点均匀分散、齐整可比，每一列中每种数字出现的次数都相等，即每种状态的取值次数相等。例如，在表2-21中，每一列都是取2个0和2个1；在表2中，第1～4列中，0和1的取值个数都是4，在第5列中，0、1、2、3的取值个数均为2。此外，任意两列组成的对数出现的次数相等，例如，在表2中，第1～2列共组成4对数据：(1,1)、(1、0)、(0、1)、(0,0)，这4对数据各出现一次，其他任意两列也如此；在表2中，第1～2列组成的数据对有4个：(0，0)、(0,1)、(1,0)、(1,1)，这4对数据出现的次数各为2次。在正交表中，每个因子的每个水品与另一个因子的各水平都“交互”一次，这就是整交性，它保证了实验点均为分散在因子与水品的组合之中，因此具有很强的代表性。

对于受多因子多水平影响的软件，正交实验法可以高效适量地生成测试用例，减少测试工作量，并且利用正交实验法得到的测试用例具有一定的覆盖度，检错率可达50%以上。正交实验法虽然好用，但在选择正交表时要注意先要确定实验因子、状态及它们之间的交互作用，选择合适的正交表，同时还要考虑实验的精度要求、费用、时长等因素。